Introduction
Historical overview
Transit light curves are an essential tool used for the detection of exoplanets. To date, there have been over 4,300 confirmed planets discovered in over 3,400 different star systems, with an additional 2,400 candidates currently awaiting follow-up analysis and validation.[1] Since the first confirmed discovery of an exoplanet – as part of a multi-planetary system in 1992 (Wolszczan and Frail, 1992), and the first exoplanet discovered around a Sun-like star shortly after in 1995 (Mayor and Queloz, 1995) – there has been an explosion in new discoveries, thanks in large part to the successful Kepler/K2 and TESS space missions. The large majority of these planets have been detected via the transit method:
Transit method
This method works by observing the dimming in apparent brightness of a star as a planet passes in front of it from our point of view. The plot of the star's brightness as a function of time defines the white light curve as seen in the schematic below:
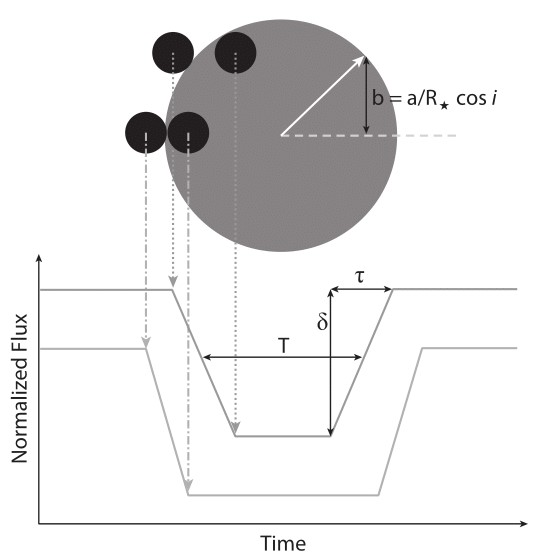
"How Do You Find an Exoplanet?" by John Asher Johnson
Even just starting with a simple single planet system in a circular orbit, there is already a wealth of information encoded in this diagram. These observations give us insight not only into the bulk properties of the planet, but into the architecture of its orbital system and characteristics of its host star as well. For example, direct observables from the light curve like the transit duration $(T)$ and ingress/egress time $(\tau)$ give us information about how tilted its orbit is and how fast the planet is traveling, while the transit depth $(\delta)$ gives us a direct measure of the size of the planet relative to its star. For circular orbits, these are nicely summarized by:
\[\begin{aligned} \frac{R_\text{p}}{R_*} &= \delta^{1/2} \\ b^2 &= 1 - \delta^{1/2}\frac{T}{t} \\ \frac{a}{R_*} &= \frac{P\delta^{1/4}}{2\pi} \left(\frac{4}{T\tau}\right)^{1/2} \\ \rho_* &= \frac{3P}{G\pi^2}\left(\frac{\delta^{1/4}}{\sqrt{T\tau}}\right)^3 \quad, \end{aligned}\]
where $P$ is the period of the planet's orbit and $a$ its semi-major axis, $b$ is the impact parameter, $R_*$ is the radius of its star, and $\rho_*$ is the stellar density.
Limb darkening
Not shown above is an added dimension that Transits.jl excels in, limb darkening, demonstrated in the schematic below:

This effect is intimately related to the shape of the light curve, and allows us to constrain the brightness profile of the star itself. As we will see next, the method of transit light curves is not just useful for the detection of exoplanets, but also for taking it to the next step of characterizing its atmosphere.
Transmission spectroscopy
If we perform the technique of transit light curve modeling on a wavelength-by-wavelength basis, we can further probe the properties of the host star and begin to make predictions about the properties of the planet's atmosphere, such as its chemical composition and whether clouds/hazes are likely to be present at higher altitudes. This analysis begins in the same way as with the white light curve seen above, only now a wavelength binned light curve is measured at a range of different wavelengths:
 Adapted from Weaver et al. (2021, submitted)
Adapted from Weaver et al. (2021, submitted)
Plotting these wavelength dependent transit depths then builds a transmission spectrum, which is filled with information about the planet's atmosphere and its star, summarized below:
Performing forward modeling (see, e.g., Kempton et al. (2017), Goyal et al. (2018)) and retrievals (see, e.g., Barstow et al. (2020) and references therein) using these frameworks then allows us to explore exoplanetary atmospheres in never before seen detail.
Summary
The detection and characterization of exoplanets through their transit light curves is a relatively new technique in the field of astronomy, with recent advances only being made possible through novel uses of large, ground-based telescopes and soon in the future with planned ELTs and space based missions like JWST. Studies using these observing facilities will require the fast and precise computation of transit light curves, which Transits.jl aims to provide.
Footnotes and references
- Barstow, J. K.; Changeat, Q.; Garland, R.; Line, M. R.; Rocchetto, M. and Waldmann, I. P. (2020). A comparison of exoplanet spectroscopic retrieval tools. Monthly Notices of the Royal Astronomical Society 493, 4884–4909, arXiv:2002.01063 [astro-ph.EP].
- Benneke, B. and Seager, S. (2012). Atmospheric Retrieval for Super-Earths: Uniquely Constraining the Atmospheric Composition with Transmission Spectroscopy. The Astrophysical Journal 753, 100, arXiv:1203.4018 [astro-ph.EP].
- Goyal, J. M.; Mayne, N.; Sing, D. K.; Drummond, B.; Tremblin, P.; Amundsen, D. S.; Evans, T.; Carter, A. L.; Spake, J.; Baraffe, I.; Nikolov, N.; Manners, J.; Chabrier, G. and Hebrard, E. (2018). A library of ATMO forward model transmission spectra for hot Jupiter exoplanets. Monthly Notices of the Royal Astronomical Society 474, 5158–5185, arXiv:1710.10269 [astro-ph.EP].
- Johnson, J. (2015). How Do You Find an Exoplanet? Princeton Frontiers in Physics (Princeton University Press).
- Kempton, E. M.-R.; Lupu, R.; Owusu-Asare, A.; Slough, P. and Cale, B. (2017). Exo-Transmit: An Open-Source Code for Calculating Transmission Spectra for Exoplanet Atmospheres of Varied Composition. Publications of the Astronomical Society of the Pacific 129, 044402, arXiv:1611.03871 [astro-ph.EP].
- Mayor, M. and Queloz, D. (1995). A Jupiter-mass companion to a solar-type star. Nature 378, 355–359.
- Rackham, B. V.; Apai, D. and Giampapa, M. S. (2018). The Transit Light Source Effect: False Spectral Features and Incorrect Densities for M-dwarf Transiting Planets. The Astrophysical Journal 853, 122, arXiv:1711.05691 [astro-ph.EP].
- Wolszczan, A. and Frail, D. (1992). A planetary system around the millisecond pulsar PSR1257 + 12. Nature 355, 145–147.
- 1https://exoplanetarchive.ipac.caltech.edu/


